Presentation on Eigenvalue Problem

Discussion Outline

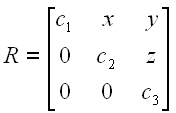
This presentation will discuss the following three topics:

1. The Importance of the Eigenvalue Problem in Science and Engineering
2. Definition of the Algebraic Eigenvalue Problem and the Need for Numerical/Computational Techniques
3. Numerical Solution Techniques

Importance - Why solve the eigenvalue problem?

The eigenvalue problem has applications many fields, including

• Quantum Mechanics
• Control Theory
• Solid Mechanics and Stress
• The Study of Vibrations and Resonance

Definition

Given and nxn matrix A and an nx1 nonzero vector x, the n values of λ for which

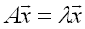
are known as the eigenvalues of A. Subtracting λx from both sides of the equation results in

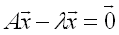
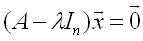
Because x is a solution to the above homogeneous system and because x≠0, the matrix

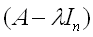
cannot be invertable and therefore

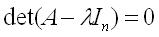
This last equation is known as the characteristic equation of A and its roots are the eigenvalues of A.

Example

Consider the triangular area shown below.

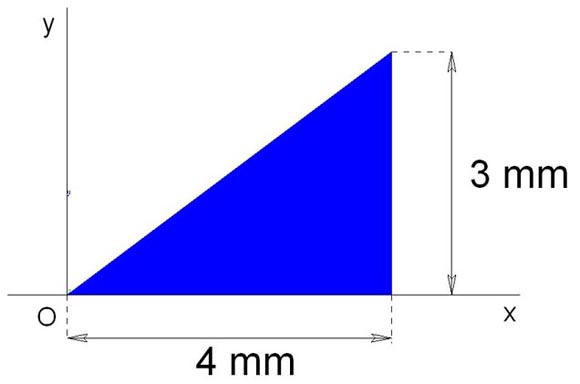
Given that the moments of Inertia of the area are

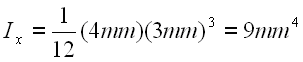
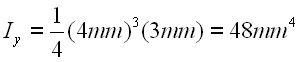
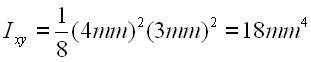
The two-dimensional moment of inertia matrix can be written as

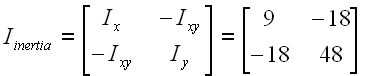
so that the eigenvalues are the area's principal momements of inertia. Using det(A-λI_n)=0, the characteristic equation is

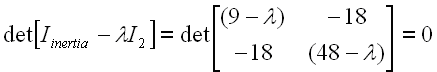
In polynomial form,

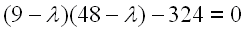
The principal moments of inertia are therefore

Limitations

1. Finding the determinants of matrices (even if small) is computationally expensive ( O(3) ).
2. If A happens to have n≥5, then det(A - λI_n ) will be a polynomial of degree n≥5.

Numerical Techniques

The Power Method

• Advantages
• Easy to understand and code
• Can be used to find one eigenvalue and its (usually the dominant eigenvalue λ₁) associated eigenvector simultaneously
• Disadvantages
• Converges slowly unless a good approximation of the eigenvector associated with λ₁ is known
• λ₁ can neither be a repeated root nor a complex root of the characteristic equation

QR Method

• Advantages
• Generally converges very quickly
• Finds all eigenvalues simultaneously
• Disadvantages
• More challenging to understand and code than power method

Special Matrices

Similar Matricies

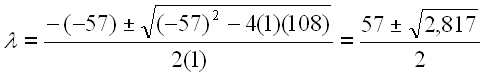
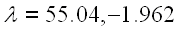
Two matrices A and B are similar and have the same eigenvalues if there is an invertible matrix P such that

Orthogonal Matrices

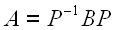
If a matrix Q is orthogonal, then

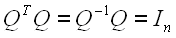
(i.e., the transpose of Q is the inverse of Q)

Triangular Matrices

A triangular matrix R can come in two flavors. The first is called lower triangular, in which all entries above the main diagonal are zero. The second is called upper triangular, in which all the entries below the main diagonal are zero.

Triangular matricies have a lot of interesting properties. For example, the transpose of a lower triangular matrix is an upper triangular matrix and vice versa. Also, the diaganal entries of a triangular matrix R are the eigenvalues of R.

Example - Upper Triangular Matrix

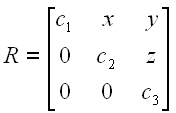
The eigenvalues of R are c₁, c₂, and c₃.

QR Algorithm

Starting with an n x n symmetric matrix A₁, the QR factorization technique begins by factoring or decomposing A₁ into an orthogonal matrix Q₁ and an upper right triangular matrix R₁ to obtain

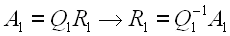
Multiplying R₁ from the right by Q₁ results in a second matrix.

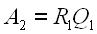
Substituting gives

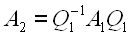
More generally,

Comments

• A shift quantity s can be introduced to speed up convergence. This method is sometimes called the sigle-shift algorithm.
• Even with shifting, the cost of a QR transformation is still very high using this approach. A better technique is to reduce A to Hessenberg form before decomposing A into Q and R components. The result higher effeciency and faster convergence.

Example

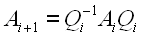
The matrix A has eigenvalues of 0, 1, 2, and 3

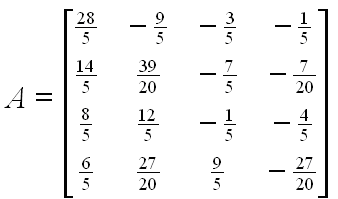
Result of 1 iteration:

Result of 2 iterations:

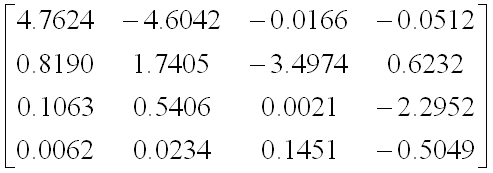
Result of 8 iterations:

After 8 iterations, all but two zeros have emerged completely and one eigenvalue has been computed to full accuracy.

Summary

• The eigenvalue problem has applications across a diverse range of quantitative fields
• For very small n the definition may be used as a solution technique. For 2 < n < 5 the definition is cumbersome and unnecessary. For n≥5 the definition is at best inadequate.
• The QR method is a fast, modern solution technique that can be used find all the eigenvalues of a matrix simultaneously.