Solution to Bernoulli’s Differential Equation

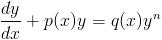
I cannot remember ever having to solve a Bernoulli differential equation outside of a formal course in ordinary differential equations, but I found this solution on an old thumb drive, and I happen to have written it in html format, so now you can enjoy it, too.

Assumption

A nonlinear ODE of the form

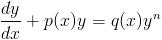(1)

Can be reduced to a linear differential equation using the substitution

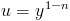(2)

Where n is any real number. Of course if n=1 or n=0, then the equation is already linear and no substitution is necessary.

Proof

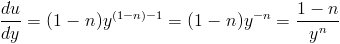
Solving for dy/du results in

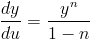(3)

By the chain rule the first derivative of y with respect to x can be written as

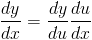
And so using (3) the first derivative of y can be rewritten as

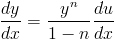(4)

Substituting (4) into Bernoulli’s equation produces the rather spongy looking expression

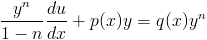
But when you multiply both sides by 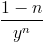something interesting emerges.

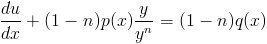(5)

Notice

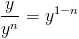
Which is the same as the original substitution that

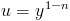
So (5) is actually just a regular old first order linear differential equation that can be solved using any known technique. In fact (5) is just the familiar standard form of a linear equation. To see this let

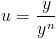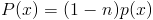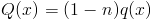then (5) becomes

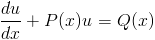(6)

Procedure for Solving a Bernoulli Differential Equation

1. Massage the equation you have into the form shown in (1)
2. Find P(x) and Q(x) and then substitute into (6)
3. Solve the resulting first-order linear ODE
4. Back substitute for u using (2) to get a solution

Example

Solve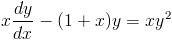     

Solution:

Step 1 of 4

Divide both sides by x to get the form shown in (1).

Step 2 of 4

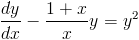
Note that:

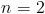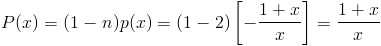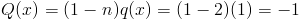Substituting P(x) and Q(x) into (6) gives

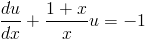(7)

Step 3 of 4

The integrating factor for this last equation on, say, (0,∞) is

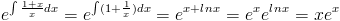
Multiplying both sides of (7) by this result gives

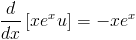
After integrating both sides you have

Step 4 of 4

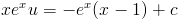
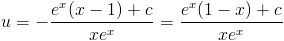
Finally back substituting yields a solution to y
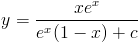